完全なチェーンとチェーンのセクションに関するオームの法則：数式のオプション、説明、説明

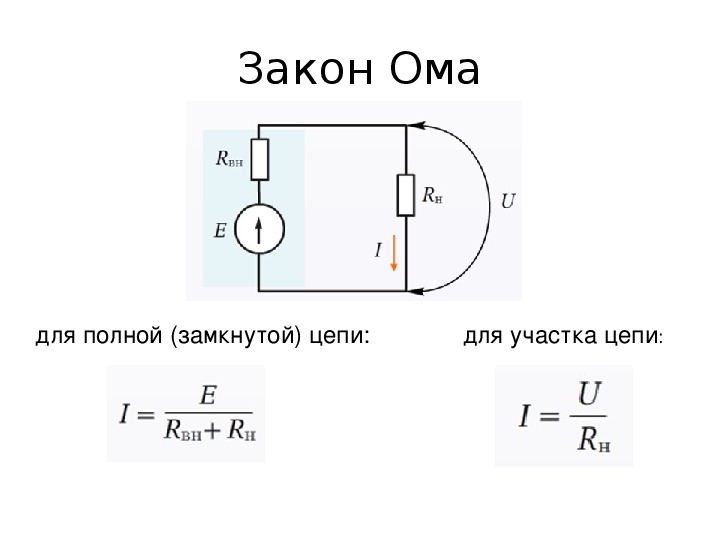
閉回路用

閉回路とは、電流が循環する閉電気接続を意味します。一連のワイヤーが相互に接続され、円の一方の端からもう一方の端まで走るように回路を完成させると、それは閉回路になります。

EMF（E）-ボルトで表され、測定され、時変磁場が電流を誘導すると述べているファラデーの法則に従って、バッテリーまたは磁力によって生成される電圧を指します。

次に：E = IR + Ir

E \ u003d I（R + r）

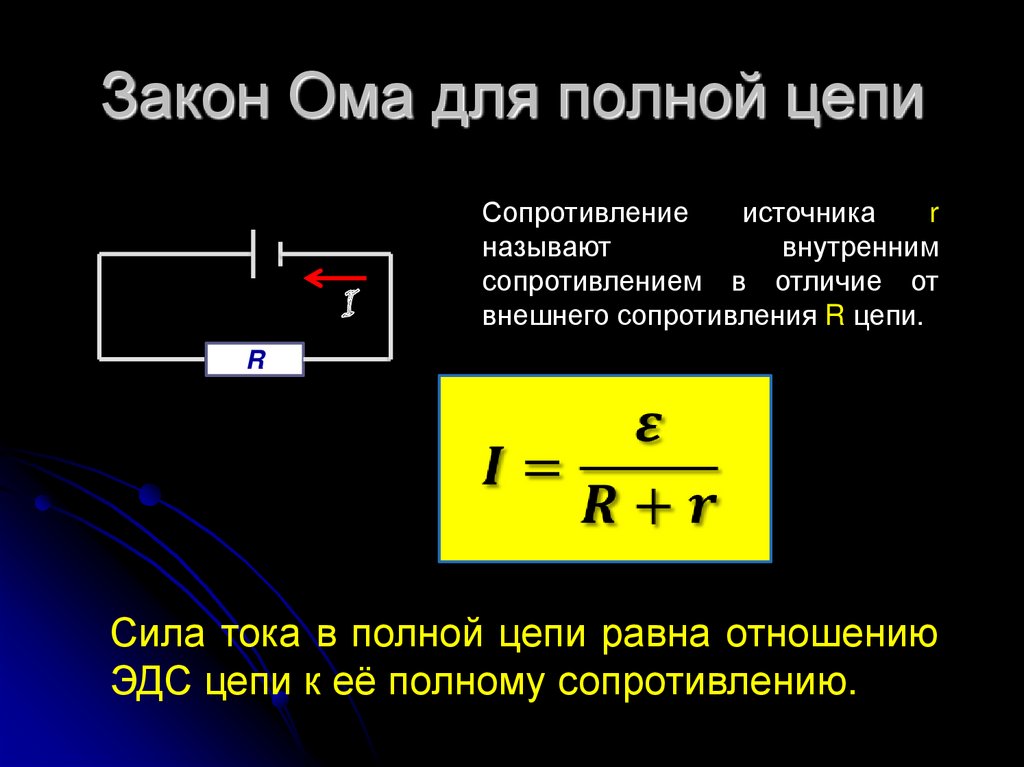
I \ u003d E /（R + r）

ここで、rは電流源の抵抗です。

この式は、オームの閉ループ回路の法則として知られています。

異種チェーン

別のセクションと完全な電気回路

セクションまたは回路全体に適用されるオームの法則は、2つの計算オプションで考慮することができます。

• 別の短いセクション。これは、EMFソースのない回路の一部です。
• 1つ以上のセクションで構成される完全なチェーン。これには、独自の内部抵抗を持つEMFソースも含まれます。

電気回路の電流セクションの計算

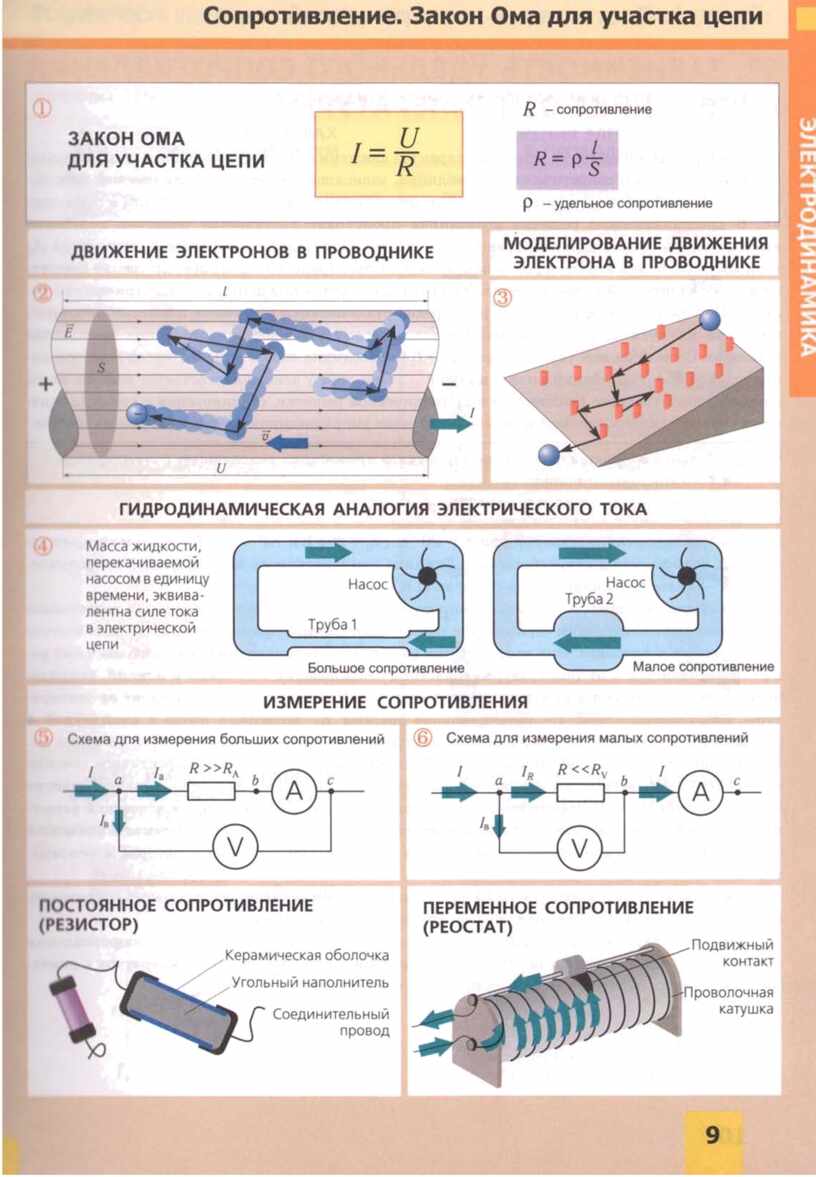
この場合、基本式I \ u003d U / Rが適用されます。ここで、Iは電流強度、Uは電圧、Rは抵抗です。それによると、オームの法則の一般的に受け入れられている解釈を定式化することができます：

この公式は、グラフィックデザインのいわゆる「カモミール」で提示される他の多くの公式の基礎となっています。セクターPでは電力が決定され、セクターI、U、Rでは電流強度、電圧、抵抗に関連するアクションが実行されます。

基本式と追加式の両方の各式を使用すると、回路での使用を目的とした要素の正確なパラメーターを計算できます。

電気回路を扱う専門家は、図に示す三角形の方法を使用して、パラメータのいずれかをすばやく決定します。

計算では、セクションの要素を接続する導体の抵抗を考慮に入れる必要があります。それらは異なる材料で作られているため、このパラメータはそれぞれの場合で異なります。完全な回路を形成する必要がある場合は、主な式に、バッテリーなどの電圧源のパラメーターが追加されます。

完全なチェーンの計算オプション

完全な回路は、電圧源（EMF）とともに単一の全体に結合された個々のセクションで構成されます。したがって、セクションの既存の抵抗は、接続されたソースの内部抵抗によって補完されます。したがって、前述の主な解釈は次のようになります。I = U /（R + r）。ここでは、EMFソースの抵抗インジケータ（r）がすでに追加されています。

純粋な物理学の観点から、この指標は非常に小さい値と見なされます。ただし、実際には、複雑な回路や回路を計算する場合、追加の抵抗が作業の精度に影響を与えるため、専門家はそれを考慮に入れる必要があります。さらに、各ソースの構造は非常に不均一であるため、場合によっては抵抗を非常に高いレートで表すことができます。

上記の計算は、DC回路に関連して実行されます。交流によるアクションと計算は、異なるスキームに従って行われます。

変数に対する法の影響

交流の場合、回路の抵抗は、アクティブ抵抗と無効抵抗負荷で構成される、いわゆるインピーダンスになります。これは、誘導特性と正弦波電流値を持つ要素の存在によるものです。電圧も可変であり、スイッチングの法則に従って動作します。

したがって、オームの法則のAC回路設計は、特定の効果を考慮して計算されます。つまり、電圧からの電流の大きさの進みまたは遅れ、および有効電力と無効電力の存在です。次に、リアクタンスには誘導性または容量性成分が含まれます。

これらの現象はすべて、式Z \ u003d U/IまたはZ\u003d R + J *（XL-XC）に対応します。ここで、Zはインピーダンスです。 R-アクティブロード; XL、XC-誘導性および容量性負荷; Jは補正係数です。

完全な回路のEMFソース

閉回路で電流が発生するためには、この回路には、極間で電荷を転送する作業が行われる特別な要素が少なくとも1つ含まれている必要があります。この要素の内部で電荷を運ぶ力は、電界に対してそうします。つまり、それらの性質は電気とは異なる必要があります。したがって、そのような力はサードパーティと呼ばれます。

米。 1.物理学における外力。

外力が電界の作用に逆らって電荷を伝達するように働く電気回路の要素は、電流源と呼ばれます。その主な特徴は外力の大きさです。それを特徴づけるために、特別な手段が導入されます-起電力（EMF）、それは文字$ \ mathscr{E}$で示されます。

電流源のEMFの値は、この電荷の値に対する電荷の移動のための外力の比率に等しくなります。

$$ \ mathscr {E} = {A_ {st} \ over q} $$

EMFの意味は電圧の意味に非常に近いため（電圧は、電荷を運ぶ電界によって行われる仕事とこの電荷の値の比率です）、EMFは、電圧と同様に、次のように測定されます。ボルト：

$$ 1B = {J \ overCl} $$

実際の電流源の2番目に重要な電気的特性は、その内部抵抗です。電荷が端子間を移動するとき、それらはEMF源の物質と相互作用するため、電流源にもある程度の抵抗があります。通常の抵抗と同様に、内部抵抗はオームで測定されますが、ラテン文字の小さい$r$で示されます。

米。 2.電流源の例。

R-電気抵抗

抵抗は電圧の逆数であり、流水中の動きに対して体を動かす効果と比較することができます。 Rの単位はOmで、ギリシャ文字の大文字Omegaで表されます。

抵抗の逆数（1 / R）は導電率として知られており、シーメンスの単位で表される、電荷を伝導するオブジェクトの能力を測定します。

使用される幾何学的に独立した量は抵抗率と呼ばれ、通常ギリシャ語の記号rで表されます。

追加情報。オームの法則は、電力の計算を簡素化する、電気ネットワークの動作の3つの重要な指標を確立するのに役立ちます。ダイオード、トランジスタなどの要素を持つ片側ネットワークには適用できません。また、サイリスタが例である非線形要素には適用できません。これらの要素の抵抗値は、与えられた電圧と電流が異なると変化するためです。

より高い周波数では、分散動作が支配的になります。同じことが非常に長い電力線でも起こります。 60 Hzの低い周波数でも、30kmなどの非常に長い伝送線路は分散した性質を持っています。主な理由は、回路を伝播する有効な電気信号が電磁波であり、電磁波に感染しているボルトやアンペアではないことです。導体は単に波のガイドとして機能します。したがって、たとえば、同軸ケーブルは、DC抵抗が無視できる場合でも、Z=75オームを示します。

オームの法則は、電気工学の基本法則です。それはすべての電気回路および電子部品で多くの実用的なアプリケーションを持っています。

オームの法則の適用の最も一般的な例：

1. 電気ヒーターに供給される電力。ヒーターコイルの抵抗と印加電圧を考慮して、そのヒーターに供給される電力を計算できます。
2. ヒューズの選択。これらは、電子機器と直列に接続された保護コンポーネントです。ヒューズ/CBの定格はアンペアです。現在のヒューズ定格は、オームの法則を使用して計算されます。
3. 電子機器の設計。ラップトップや携帯電話などの電子機器には、特定の定格電流のDC電源が必要です。一般的な携帯電話のバッテリーには0.7〜1Aが必要です。これらのコンポーネントを流れる電流の速度を制御するために、抵抗が使用されます。オームの法則は、一般的な回路の定格電流を計算するために使用されます。

かつて、オームの結論は電気の分野での新しい研究のきっかけとなりましたが、現代の電気工学はそれらに基づいているため、今日ではその重要性を失っていません。 1841年、オムは王立学会の最高の栄誉であるコプリメダルを授与され、「オム」という用語は早くも1872年に抵抗の単位として認識されました。

DC回路の不均一なセクション

異種構造には回路のそのようなセクションがあり、導体と要素に加えて、電流源があります。この領域の総電流強度を計算するときは、そのEMFを考慮に入れる必要があります。

異種サイトの主なパラメータとプロセスを定義する式があります：q = q0 xnxV。そのインジケータは次のように特徴付けられます。

• 電荷（q）を動かす過程で、それらは特定の密度を獲得します。その性能は、導体（S）の電流強度と断面積に依存します。
• 一定の濃度（n）の条件下では、単一の期間に移動した単位電荷（q0）の数を正確に示すことができます。
• 計算では、導体は条件付きである程度の体積（V）のある円筒形のセクションと見なされます。

導体をバッテリーに接続すると、しばらくするとバッテリーが放電します。つまり、電子の動きは徐々に遅くなり、最終的には完全に停止します。これは、導体の分子格子によって促進されます。これは、電子同士の衝突やその他の要因を打ち消します。このような抵抗を克服するには、特定のサードパーティの力を追加で適用する必要があります。

計算中に、これらの力はクーロン力に追加されます。また、単位電荷qを1点目から2点目に移すには、A1-2または単にA12の作業を行う必要があります。この目的のために、電位差（ϕ1-ϕ2）が作成されます。直流電流源の作用下でEMFが発生し、回路に沿って電荷が移動します。総応力の大きさは、上記のすべての力で構成されます。

計算では、DC電源への接続の極性を考慮する必要があります。端子を変更すると、EMFも変更され、電荷の移動が加速または減速します。

要素のシリアルおよびパラレル接続

電気回路の要素（回路のセクション）の場合、特徴的なモーメントは直列または並列接続です。

したがって、各タイプの接続には、電流の流れと電圧供給の性質が異なります。このため、オームの法則は、要素を含めるオプションに応じて、さまざまな方法で適用されます。

直列接続された抵抗素子のチェーン

直列接続（2つのコンポーネントを持つ回路のセクション）に関しては、次の表現が使用されます。

• I = I₁ =私₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

この定式化は、直列に接続された抵抗性コンポーネントの数に関係なく、回路のセクションを流れる電流の値が変化しないことを明確に示しています。

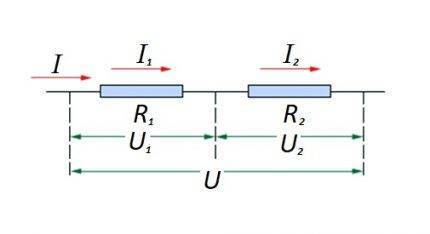回路セクションの抵抗素子を互いに直列に接続します。このオプションには独自の計算法則があります。図の場合：I、I1、I2-電流の流れ。 R1、R2-抵抗要素; U、U1、U2-印加電圧

回路のアクティブな抵抗性コンポーネントに印加される電圧の量は合計であり、EMFソースの値に加算されます。

この場合、個々のコンポーネントの電圧はUx = I*Rxです。

総抵抗は、回路のすべての抵抗成分の値の合計と見なす必要があります。

並列接続された抵抗素子のチェーン

抵抗膜方式のコンポーネントが並列接続されている場合、ドイツの物理学者オームの法則に関して、定式化は公正であると見なされます。

• I = I₁ +私₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

「混合」タイプの回路セクションをコンパイルするためのオプションは、並列およびシリアル接続が使用されている場合は除外されません。

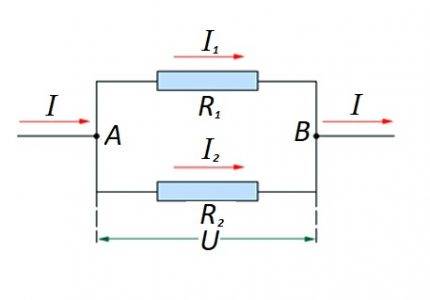回路セクション内の抵抗素子の相互並列接続。このオプションには、独自の計算法則が適用されます。図の場合：I、I1、I2-電流の流れ。 R1、R2-抵抗要素; U-印加電圧; A、B-入口/出口ポイント

このようなオプションの場合、計算は通常、並列接続の抵抗定格の初期計算によって実行されます。次に、直列に接続された抵抗の値が結果に追加されます。

法の積分形式と微分形式

計算に関する上記のすべての点は、いわば「均質な」構造の導体が電気回路の一部として使用される条件に適用できます。

一方、実際には、導体の構造がさまざまな領域で変化する回路図面の構築に対処しなければならないことがよくあります。たとえば、より大きな断面のワイヤーが使用されたり、逆に、より小さなワイヤーが異なる材料に基づいて作られたりします。

このような違いを考慮に入れるために、いわゆる「微分積分オームの法則」のバリエーションがあります。無限に小さい導体の場合、電流密度レベルは強度と導電率の値に応じて計算されます。

微分計算では、次の式が使用されます。J=ό*E

積分計算の場合、それぞれ次のようになります。I *R=φ1-φ2+έ

ただし、これらの例は高等数学の学校にかなり近く、単純な電気技師の実際の実践では実際には使用されていません。

電流と抵抗を理解する

電流の概念から始めましょう。要するに、金属に関連する電流は、電子の方向付けられた動き、つまり負に帯電した粒子です。それらは通常、小さな円として表されます。落ち着いた状態で、彼らはランダムに動き、絶えず方向を変えます。特定の条件下（電位差の出現）では、これらの粒子は特定の方向に特定の動きを開始します。この動きが電流です。

より明確にするために、ある平面にこぼれた水と電子を比較することができます。飛行機が静止している限り、水は動きません。しかし、傾斜が現れるとすぐに（電位差が生じた）、水は動き始めました。電子も同じです。

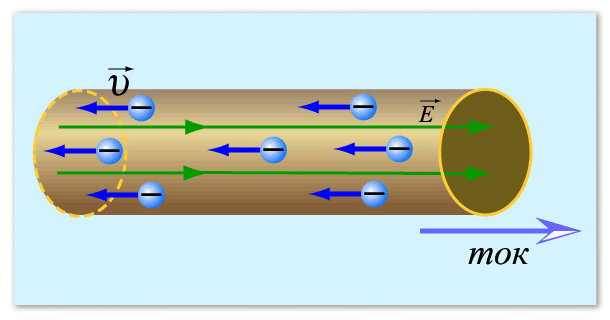
これが電流の想像方法です

ここで、抵抗とは何か、なぜ電流強度でフィードバックがあるのか​​を理解する必要があります。抵抗が高いほど、電流は低くなります。ご存知のように、電子は導体を通って移動します。金属は電気を通す優れた能力を持っているので、通常これらは金属線です。金属には緻密な結晶格子があることを私たちは知っています：近くにあり、相互接続されている多くの粒子。電子は金属原子の間を通り抜けて衝突し、移動を困難にします。これは、導体が及ぼす抵抗を説明するのに役立ちます。ここで、抵抗が高いほど電流強度が低くなる理由が明らかになります。粒子が多いほど、電子が経路を通過するのが難しくなり、通過が遅くなります。これは整理されたようです。

この依存関係を経験的にテストしたい場合は、可変抵抗器を見つけ、抵抗器（電流計）を電流源（バッテリー）に直列に接続します。スイッチを回路に挿入することも望ましいです-通常のトグルスイッチ。

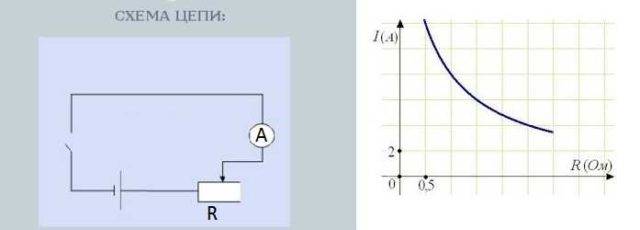
電流の抵抗への依存性をテストするための回路

抵抗ノブを回すと抵抗が変わります。同時に、電流強度を測定する電流計の読み取り値も変化します。さらに、抵抗が大きいほど、矢印のずれが少なくなり、電流が少なくなります。抵抗が低いほど、矢印のずれが大きくなり、電流が大きくなります。

電流の抵抗への依存性はほぼ線形です。つまり、グラフにはほぼ直線として反映されます。なぜほとんど-これは別々に議論されるべきですが、それは別の話です。

交流のオームの法則

AC回路を計算するとき、抵抗の概念の代わりに、「インピーダンス」の概念が導入されます。インピーダンスは文字Zで表され、負荷Rの有効抵抗が含まれます。_a およびリアクタンスX（またはR_r）。これは、正弦波電流（およびその他の形式の電流）の形状、誘導性要素のパラメーター、およびスイッチングの法則によるものです。

1. 誘導回路の電流は瞬時に変化することはありません。
2. 静電容量のある回路の電圧は、瞬時に変化することはありません。

したがって、電流は電圧より遅れたり進んだりし始め、見かけの電力はアクティブとリアクティブに分けられます。

U = I / Z

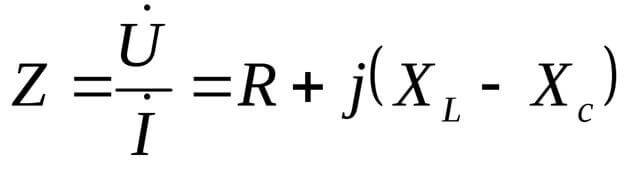
バツ_L およびX_C 負荷の無効成分です。

この点で、値cosФが導入されます。

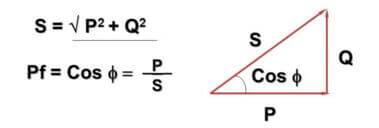
ここで-Q-交流および誘導容量コンポーネントによる無効電力、P-有効電力（アクティブコンポーネントで消費）、S-見かけの電力、cosФ-力率。

式とその表現がピタゴラスの定理と交差していることに気づいたかもしれません。これは真実であり、角度Фは負荷の無効成分がどれだけ大きいかに依存します-それが大きいほど、それは大きくなります。実際には、これは、企業が全電力を支払う一方で、ネットワークを実際に流れる電流が家庭用メーターで考慮される電流よりも大きいという事実につながります。

この場合、抵抗は複雑な形で表されます。

ここで、jは虚数単位であり、複雑な形式の方程式に典型的です。あまり一般的にはiと呼ばれませんが、電気工学では、交流の実効値も示されます。したがって、混乱しないように、jを使用することをお勧めします。

虚数単位は√-1です。二乗するときにそのような数がないことは論理的であり、「-1」の負の結果になる可能性があります。

オームの法則が発生したとき

理想的な条件を作るのは簡単ではありません。純粋な導体でも、電気抵抗は温度によって変化します。その減少は、結晶格子の分子の活動を最小限に抑え、自由電荷の移動を単純化します。あるレベルの「凍結」では、超伝導の影響が発生します。加熱すると逆の効果（導電率の低下）が見られます。

同時に、電解質、金属、および特定の種類のセラミックは、電流密度に関係なく電気抵抗を保持します。特定の温度レジームを維持しながらパラメータを安定させることにより、追加の修正なしでオームの法則の式を適用することが可能になります。

半導体材料とガスは、電気抵抗が変化することを特徴としています。このパラメータは、コントロールボリュームの電流強度に大きく影響されます。性能特性を計算するには、特殊な計算方法を適用する必要があります。

交流を考慮した場合、計算方法を修正します。この場合、反応性成分の存在を考慮に入れる必要があります。抵抗の抵抗性により、オームの法則の公式に基づいて考慮された計算技術を適用することが可能です。

キルヒホッフの法則。

分布
電気回路の分岐の電流
キルヒホッフの最初の法則に従い、
およびセクション全体の応力の分布
チェーンはキルヒホッフの第二法則に従います。

キルヒホッフの法則
オームの法則とともにメインです
電気回路の理論で。

最初
キルヒホッフの法則：

代数
ノードの電流の合計はゼロです。

_私
= 0 (19)

どこ
私
特定のノードに収束するブランチの数です。

つまり、合計
ブランチの電流に拡張し、
考慮されたものに収束する
ノード。

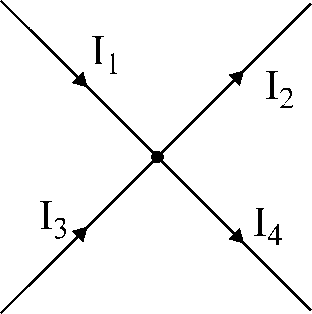
図17。図
キルヒホッフの最初の法則に。

番号
最初の式に従ってコンパイルされた方程式
キルヒホッフの法則は次の式で決定されます。

ナップ
= Nu
– 1,

どこ
Nu
考慮されるチェーン内のノードの数です。

の流れの兆候
方程式は、選択されたものを考慮して考慮されます
正の方向。でのサイン
電流が同じであれば、電流は同じです
これを基準にした
ノード。

例えば、
図17に示すノードの場合：
ノードに流れる電流に符号を割り当てます
「+」、およびノー​​ドから流れる電流へ-記号
«-».

次に、方程式
キルヒホッフの最初の法則によれば、それは書かれるでしょう
そう：

私₁
- 私₂
+私₃
- 私₄
= 0.

方程式、
キルヒホッフの最初の法則に従って編集された、
ノードと呼ばれます。

これ
法は、ノードで
電荷がたまらない
そして消費されません。電気の量
サイトに来る料金は合計に等しい
同一のノードを離れる料金
同じ期間。

2番
キルヒホッフの法則：

代数
起電力の合計どんな閉回路でも
チェーンは、滝の代数和に等しい
この回路の要素の電圧：

Ui
= 
エイ

IiRi=Ei（20）

どこ
私
-要素番号（抵抗または
考慮される電圧源）
輪郭。

**番号
2番目に従ってコンパイルされた方程式
キルヒホッフの法則は次の式で決定されます。

ナップ
= Nb
-Nu
+ 1 – Ned.s.

どこ
Nb
-電気回路の分岐数。

Nu
—ノードの数。

Ned.s.
理想的なemfソースの数です。

図18。図
キルヒホッフの第二法則に。

為に、
第二法則を正しく書くために
与えられた輪郭のキルヒホッフは、次のようになります
次のルールに準拠します。

1. 任意に
   等高線バイパスの方向を選択し、
   たとえば、時計回りです（図18）。

2. emf
   と一致する電圧降下
   選択した方向の方向に
   バイパスは次の式で記述されます
   記号「+」; e.f.s.と電圧降下
   方向が合わない
   輪郭、それからそれらは記号によって前に置かれます
   «-».

例えば、
図18の等高線については、キルヒホッフの第2法則
次のように書かれます：

U₁
– u₂
+ U₃
= E₁
– e₃
– e₄
(21)

式（20）は次のようになります。
次のように書き直します：

（Ui
– ei）
= 0 (22)

どこ
（U
– e）
-枝の張り。

その結果、
キルヒホッフの第二法則を定式化することができます
次のように：

代数
任意の分岐の電圧の合計
閉ループはゼロです。

潜在的な
前に説明した図は
2番目のグラフィカルな解釈
キルヒホッフの法則。

タスク番号1。

で
図1の回路には電流Iが与えられています₁
そして私₃,
抵抗と起電力電流を決定する
私₄,
私₅,
私₆
;ポイント間の電圧
およびb
もし私が₁
= 10mA、
私₃
= -20 mA、
R₄
= 5kOhm、
E₅
= 20B、
R₅
= 3kOhm、
E₆
= 40B、
R₆
=2kOhm。

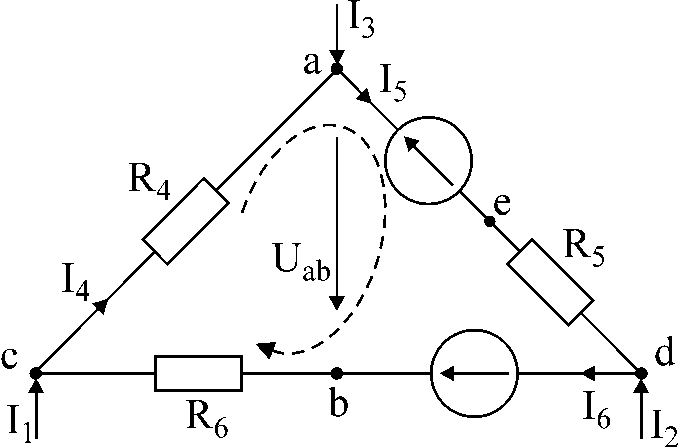
図1

解決：

1. 与えられた
   輪郭、次のように2つの方程式を構成します
   キルヒホッフの最初の法則と1つ-によると
   2番目。輪郭方向
   矢印で示されています。

で
私たちが得る解決策の結果として：私は₆
= 0;私₄
= 10mA;
私₅
= -10mA

1. 聞く
   ポイント間の電圧方向
   a
   およびb
   ポイント「a」から
   「b」を指す
   — u_ab.
   この電圧は次の式から求めることができます
   キルヒホッフの第二法則：

私₄R₄
+ U_ab
+私₆R₆
= 0

U_ab
=-50V。

タスク番号2。

為に
図2の図は、に従って方程式を作成します。
キルヒホッフの法則と未知数を決定する
ポイント。

与えられた：
私₁
= 20mA;
私₂
= 10mA

R₁
= 5kOhm、
R₃
= 4kOhm、
R₄
= 6kOhm、
R₅
= 2kOhm、
R₆
=4kΩ。

図2

解決：

ノードの数
方程式-3、等高線方程式の数
– 1.

覚えて！
2番目に従って方程式をコンパイルするとき
キルヒホッフの法則、輪郭を選択します。
これには電流源は含まれていません。
輪郭の方向は図に示されています。

で
この回路の、ブランチの電流I₁
そして私₂.
わからない
電流
私₃,
私₄,
私₅,
私₆.

決定する
システム、私たちは得る：私₃
= 13.75 mA;
私₄
= -3.75mA;
私₅
= 6.25mA;
私₆
=16.25mA。

基本概念

閉回路が電子を回路内の高電位から低電位に移動させると、電流が流れます。言い換えれば、電流は、それらを動かすためのエネルギーを持っている電子源と、それらの不足によって特徴付けられる負電荷のそれらの戻り点を必要とします。物理現象として、回路の電流は3つの基本的な量によって特徴付けられます。

• 電圧;
• 現在の強さ;
• 電子が移動する導体の抵抗。

強さと緊張

電流強度（I、アンペアで測定）は、単位時間あたりに回路内の場所を移動する電子（電荷）の量です。言い換えれば、測定Iは運動中の電子の数の決定です

この用語は動きのみを指すことを理解することが重要です。たとえば、接続されていないバッテリーの端子の静電荷には、測定可能なIの値はありません。一方向に流れる電流は直接（DC）と呼ばれます。周期的に方向を変えることを交流（AC）と呼びます。電圧は、圧力などの現象、または重力の影響下にある物体の位置エネルギーの差として説明できます。

この不均衡を作り出すために、あなたは最初にエネルギーを消費しなければなりません、そしてそれは適切な状況の下で動いていることで実現されます。たとえば、高所からの負荷の落下では、負荷を持ち上げる作業が実行されます。ガルバニ電池では、発電機での化学エネルギーの変換により、端子での電位差が形成されます。電磁界

応力は、圧力などの現象、または重力の影響下にある物体の位置エネルギーの差として説明できます。この不均衡を作り出すために、あなたは最初にエネルギーを消費しなければなりません、そしてそれは適切な状況の下で動いていることで実現されます。たとえば、高所からの負荷の落下では、それを持ち上げる作業が実現されます。ガルバニ電池では、発電機での化学エネルギーの変換により、端子での電位差が形成されます。電磁界。

導体抵抗

普通の導体がどんなに優れていても、電子の動きに抵抗がなければ電子を通過させることはできません。この比較は完全ではありませんが、抵抗を機械的摩擦の類似物と見なすことは可能です。導体に電流が流れると、電位差の一部が熱に変換されるため、抵抗器の両端で常に電圧降下が発生します。電気ヒーター、ヘアドライヤー、およびその他の同様のデバイスは、電気エネルギーを熱の形で放散するためだけに設計されています。

簡略化された抵抗（Rとして示される）は、回路内で電子の流れがどれだけ遅延するかを示す尺度です。それはオームで測定されます。抵抗器またはその他の要素の導電率は、次の2つの特性によって決まります。

• ジオメトリ;
• 素材。

水流のアナロジーから明らかなように、形状は最も重要です。長くて細いパイプを通して水を押し出すことは、短くて広いパイプを通して水を押し出すことよりもはるかに困難です。材料が決定的な役割を果たします。たとえば、電子は銅線内を自由に移動できますが、形状に関係なく、ゴムなどの絶縁体を通過することはできません。形状と材料に加えて、導電率に影響を与える他の要因があります。

オームの法則の解釈

電荷の移動を確実にするには、回路を閉じる必要があります。追加の電力がない場合、電流は長期間存在できません。ポテンシャルはすぐに等しくなります。回路の動作モードを維持するには、追加の電源（発電機、バッテリー）が必要です。

完全な回路には、すべてのコンポーネントの総電気抵抗が含まれます。正確な計算のために、導体、抵抗素子、および電源の損失が考慮されます。

特定の電流強度に対してどのくらいの電圧を印加する必要があるかは、次の式で計算されます。

U = I*R。

同様に、考慮された関係の助けを借りて、回路の他のパラメータが決定されます。

パラレルおよびシリアル接続

電気では、要素は直列に（次々に、または並列に）接続されます。これは、複数の入力が1つのポイントに接続され、同じ要素からの出力が別のポイントに接続される場合です。

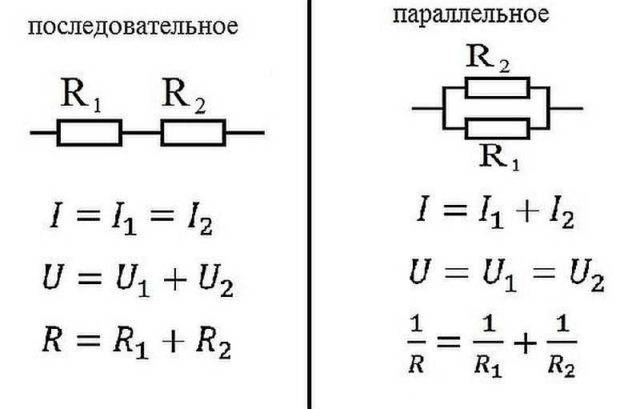
並列および直列接続に関するオームの法則

シリアル接続

これらの場合、オームの法則はどのように機能しますか？直列に接続すると、要素のチェーンを流れる電流は同じになります。直列に接続された要素を持つ回路のセクションの電圧は、各セクションの電圧の合計として計算されます。これはどのように説明できますか？エレメントを流れる電流は、電荷の一部がエレメントのある部分から別の部分に移動することです。つまり、それはいくつかの作業です。この仕事の大きさは緊張です。これがストレスの物理的な意味です。これが明らかな場合は、次に進みます。

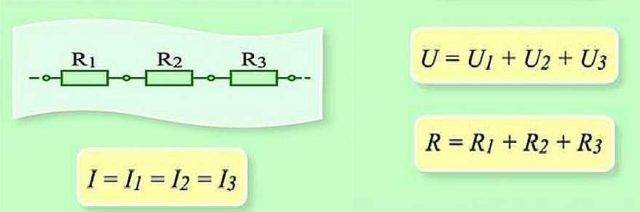
回路のこのセクションのシリアル接続とパラメータ

直列に接続する場合は、各要素を介して電荷を順番に転送する必要があります。そして、各要素で、これは特定の「ボリューム」の作業です。また、チェーンのセクション全体の作業量を見つけるには、各要素の作業を追加する必要があります。したがって、合計電圧は各要素の電圧の合計であることがわかります。

同様に、加算の助けを借りて、回路セクションの総抵抗も求められます。どうやって想像できますか？要素のチェーンを流れる電流は、すべての抵抗を順番に克服します。一つずつ。つまり、彼が克服した抵抗を見つけるには、抵抗を合計する必要があります。多かれ少なかれこのように。数学的導出はより複雑であり、この法則のメカニズムを理解するのは簡単です。

並列接続

並列接続とは、導体/要素の始点が1つのポイントに収束し、別のポイントでそれらの端が接続される場合です。このタイプの化合物に有効な法則を説明しようとします。 currentから始めましょう。エレメントの接続点には、ある程度の電流が供給されます。それは分離し、すべての導体を通って流れます。このことから、セクションの合計電流は、各要素の電流の合計に等しいと結論付けます：I = I1 + I2+I3。

さて、電圧について。電圧が電荷を動かす仕事である場合、1つの電荷を動かすために必要な仕事はどの要素でも同じです。つまり、並列接続された各要素の電圧は同じになります。 U = U1 = U2=U3。チェーンセクションのオームの法則の説明の場合ほど楽しく視覚的ではありませんが、理解できます。

並列接続の法則

抵抗については、物事はもう少し複雑です。導電率の概念を紹介しましょう。これは、電荷がこの導体を通過するのがどれほど簡単か難しいかを示す特性です。抵抗が低いほど、電流が流れやすくなることは明らかです。したがって、導電率-G-は抵抗の逆数として計算されます。式では、G = 1/Rのようになります。

なぜ導電率について話しているのですか？要素が並列に接続されているセクションの総導電率は、各セクションの導電率の合計に等しいためです。 G = G1 + G2+G3-わかりやすい。電流が並列要素のこのノードをどれだけ簡単に克服できるかは、各要素の導電率によって異なります。したがって、折りたたむ必要があることがわかります。

これで、抵抗に移ることができます。導電率は抵抗の逆数であるため、次の式を得ることができます：1 / R = 1 / R1 + 1 / R2 + 1/R3。

何が私たちにパラレルおよびシリアル接続を提供しますか？

理論的な知識は良いですが、実際にそれをどのように適用するのですか？あらゆるタイプの要素を並列および直列に接続できます。ただし、線形要素を記述する最も単純な式のみを検討しました。線形要素は抵抗であり、「抵抗」とも呼ばれます。学んだことをどのように使用できるかを次に示します。

大きな値の抵抗がないが、小さな抵抗がいくつかある場合は、いくつかの抵抗を直列に接続することで、目的の抵抗を得ることができます。ご覧のとおり、これは便利なテクニックです。
バッテリーの寿命を延ばすために、バッテリーを並列に接続することができます。この場合の電圧は、オームの法則に従って同じままです（マルチメーターで電圧を測定することで確認できます）。また、デュアルバッテリーの「寿命」は、互いに置き換わる2つの要素の「寿命」よりもはるかに長くなります。

注意：同じ電位の電源装置のみを並列に接続できます。つまり、電池切れで新しい電池を接続することはできません。

それでも接続すると、充電量の多いバッテリーは充電量の少ないバッテリーを充電する傾向があります。その結果、それらの合計料金は低い値に下がります。

一般に、これらはこれらの化合物の最も一般的な用途です。

理想的なEMFソース

起電力（E）は、電荷キャリアの閉回路での動きに対する外力の影響の程度を決定する物理的な量です。言い換えれば、電流が導体を流れる傾向がどれだけ強いかは、EMFに依存します。

そのような理解できない現象を説明するとき、国内の学校の教師は水力学的アナロジーの方法に目を向けるのが好きです。導体がパイプであり、電流がその中を流れる水の量である場合、EMFはポンプが流体をポンプするために発生する圧力です。

起電力という用語は、電圧などの概念に関連しています。彼女、EMFもボルトで測定されます（単位-「V」）。バッテリー、発電機、ソーラーパネルなど、すべての電源には独自の起電力があります。多くの場合、このEMFは出力電圧（U）に近いですが、常にそれよりわずかに低くなります。これは、電圧の一部が必然的に低下するソースの内部抵抗によって引き起こされます。

このため、EMFの理想的なソースは、バッテリーRinの内部抵抗が非常に低いものの、絶対零度とは異なるため、現実の世界には存在しない抽象的な概念または物理モデルです。

emfの理想的で実際のソース

微分形式で

導体は通常不均一であり、可能な限り最小のセクションに分割する必要があるため、式は微分形式で提示されることがよくあります。それを通過する電流は大きさと方向に関連付けられているため、スカラー量と見なされます。ワイヤを流れる合成電流が見つかるときはいつでも、すべての個々の電流の代数和が取られます。このルールはスカラー量にのみ適用されるため、電流もスカラー量と見なされます。現在のdI=jdSがセクションを通過することが知られています。その電圧はEdlであり、断面が一定で長さが等しいワイヤの場合、比率は次のようになります。

微分形式

したがって、ベクトル形式での電流の表現は次のようになります。j=E。

重要！金属導体の場合、導電率は温度の上昇とともに減少しますが、半導体の場合は増加します。オモフの法則は厳密な比例関係を示していません

金属や合金の大規模なグループの抵抗は、絶対零度に近い温度で消失し、このプロセスは超伝導と呼ばれます。